حول
Dr Mahir Zanqur
ا.د.مناهج وطرق تدريس الرياضيات
كلية تربية الوادي الجديد
علم الإحصاء Statistics Science
قديما كان يعرف الإحصاء بأنه هو العلم الذي يهتم بأساليب جمع البيانات وتنظيمها في جداول إحصائية ثم عرضها بيانياً. ومع تطور هذا العلم في العصر الحديث يمكن تعريفه تعريفاً شاملاً بأنه العلم الذي يبحث في:
- جمع البيانات والحقائق المتعلقة بمختلف الظواهر وتسجيلها في صورة رقمية وتصنيفها وعرضها في جداول منظمة وتمثيلها بيانياً، وإيجاد المقاييس الإحصائية المناسبة.
- مقارنة الظواهر المختلفة ودراسة العلاقات والاتجاهات بينها واستخدامها في فهم حقيقة تلك الظواهر ومعرفة القوانين التي تسير تبعاً لها.
- تحليل البيانات واستخراج النتائج منها ثم اتخاذ القرارات المناسبة.
وينقسم علم الإحصاء إلى قسمين أساسيين هما:
الإحصاء الوصفي Descriptive Statistics:
عبارة من مجموعة الأساليب الإحصائية التي تعنى بجمع البيانات وتنظيمها وتصنيفها وتلخيصها وعرضها بطريقة واضحة في صورة جداول أو أشكال بيانية وحساب المقاييس الإحصائية المختلفة لوصف متغير ما (أو أكثر من متغير) في مجتمع ما أو عينه منه.
الإحصاء الاستدلالي Statistics Inferential :
عبارة عن مجموعة من الأساليب الإحصائية التي تستخدم بغرض تحليل بيانات ظاهرة (أو أكثر) في مجتمع ما على أساس بيانات عينة احتمالية تسحب منه وتفسيرها للتوصل إلى التنبؤ واتخاذ القرارات المناسبة.
ويتلخص الأسلوب الإحصائي في الخطوات التالية:
1- جمع البيانات عن طريق التجربة والمشاهدة بوفرة كافية لاستخلاص النتائج منها.
2- عرض هذه البيانات بطريقة تساعد على تفهمها والاستفادة منها حيث أن البيانات الإحصائية في صورتها الأولية لا يمكن الاستفادة أو استخلاص النتائج منها وذلك في حالة وجود عدد كبير من الأرقام أو الصفات.
المجتمع Population:
هو مجموع كل المفردات الممكنة سواء كانت أفراداً أو أشياء أو وحدات تجريبية أو قياسات موضوع الاهتمام في الدراسة، وقد يتكون المجتمع من عدد محدود من المفردات أو أن يكون عدد مفرداته لا نهائي، كما أن المجتمع قد يكون حقيقيا أو افتراضيا.
الحصر الشامل Census:
هو جمع البيانات من جميع مفردات المجتمع المراد دراسته.
وفي بعض الحالات لا نتمكن من حصر كل مفردات المجتمع مثل مجتمعات الأسماك أو النباتات أو تؤدى عملية الحصول على البيانات من مفردات المجتمع إلى إهلاكها أو إتلافها وبالتالي لا يمكن جمع البيانات من كل المفردات أو قد تحتاج عملية جمع البيانات من جميع المفردات إلى وقت طويل أو جهد أو تكاليف باهظة، وفي مثل هذه الحالات يتم جمع البيانات بأخذ جزء فقط من مفردات المجتمع وهو ما يسمى بالعينة.
- جمع البيانات والحقائق المتعلقة بمختلف الظواهر وتسجيلها في صورة رقمية وتصنيفها وعرضها في جداول منظمة وتمثيلها بيانياً، وإيجاد المقاييس الإحصائية المناسبة.
- مقارنة الظواهر المختلفة ودراسة العلاقات والاتجاهات بينها واستخدامها في فهم حقيقة تلك الظواهر ومعرفة القوانين التي تسير تبعاً لها.
- تحليل البيانات واستخراج النتائج منها ثم اتخاذ القرارات المناسبة.
وينقسم علم الإحصاء إلى قسمين أساسيين هما:
الإحصاء الوصفي Descriptive Statistics:
عبارة من مجموعة الأساليب الإحصائية التي تعنى بجمع البيانات وتنظيمها وتصنيفها وتلخيصها وعرضها بطريقة واضحة في صورة جداول أو أشكال بيانية وحساب المقاييس الإحصائية المختلفة لوصف متغير ما (أو أكثر من متغير) في مجتمع ما أو عينه منه.
الإحصاء الاستدلالي Statistics Inferential :
عبارة عن مجموعة من الأساليب الإحصائية التي تستخدم بغرض تحليل بيانات ظاهرة (أو أكثر) في مجتمع ما على أساس بيانات عينة احتمالية تسحب منه وتفسيرها للتوصل إلى التنبؤ واتخاذ القرارات المناسبة.
ويتلخص الأسلوب الإحصائي في الخطوات التالية:
1- جمع البيانات عن طريق التجربة والمشاهدة بوفرة كافية لاستخلاص النتائج منها.
2- عرض هذه البيانات بطريقة تساعد على تفهمها والاستفادة منها حيث أن البيانات الإحصائية في صورتها الأولية لا يمكن الاستفادة أو استخلاص النتائج منها وذلك في حالة وجود عدد كبير من الأرقام أو الصفات.
المجتمع Population:
هو مجموع كل المفردات الممكنة سواء كانت أفراداً أو أشياء أو وحدات تجريبية أو قياسات موضوع الاهتمام في الدراسة، وقد يتكون المجتمع من عدد محدود من المفردات أو أن يكون عدد مفرداته لا نهائي، كما أن المجتمع قد يكون حقيقيا أو افتراضيا.
الحصر الشامل Census:
هو جمع البيانات من جميع مفردات المجتمع المراد دراسته.
وفي بعض الحالات لا نتمكن من حصر كل مفردات المجتمع مثل مجتمعات الأسماك أو النباتات أو تؤدى عملية الحصول على البيانات من مفردات المجتمع إلى إهلاكها أو إتلافها وبالتالي لا يمكن جمع البيانات من كل المفردات أو قد تحتاج عملية جمع البيانات من جميع المفردات إلى وقت طويل أو جهد أو تكاليف باهظة، وفي مثل هذه الحالات يتم جمع البيانات بأخذ جزء فقط من مفردات المجتمع وهو ما يسمى بالعينة.
المقاييس الإحصائية
أولاً: مقاييس النزعة المركزية Measures of Central Tendency
معظم قيم مفردات أي ظاهرة لها الرغبة في التجمع أو التمركز حول قيمة معينة تسمى القيمة المتوسطة، هذا التجمع عند هذه القيمة يسمى بالنزعة المركزية للبيانات.
أهم مقاييس النزعة المركزية:
الوسط الحسابي، الوسيط ، المنوال ،الرُبيعات، الوسط الهندسي،الوسط التوافقي.
(1) الوسط الحسابي Arithmetic Mean أو Average
الوسط الحسابي لمجموعة من القيم هو القيمة التي لو أعطيت لكل مفردة من مفردات المجموعة لكان مجموع القيم الجديدة مساويا لمجموع القيم الأصلية ويرمز له بالرمز . وستخدم الوسط الحسابي في حالة البيانات الرقمية فقط.
(2) الوسيط Median:
يعرف الوسيط لمجموعة من البيانات بأنه القيمة التي تقع في وسط المجموعة تماماً بعد ترتبيها تصاعدياً أو تنازلياً، أي هو القيمة التي تقسم مجموعة البيانات إلى قسمين بحيث يكون عدد القيم الأكبر منها مساوياً عدد القيم الأصغر منها ويرمز له بالرمز . ويستخدم الوسيط في حالة البيانات الترتيبية.
(3) المنوال Mode:
يعرف المنوال لمجموعة من البيانات بأنه القيمة الأكثر شيوعاً (تكراراً) في المجموعة ويرمز له بالرمز . يفضل استخدام المنوال في حالة البيانات الوصفية والترتيبية.
4- الرُبيعات Quartiles
يمكن تقسم المساحة تحت المضلع التكراري إلى أربعة أقسام متساوية تسمى الرُبيعات وعددها ثلاثة هي من اليسار إلى اليمين:
الرُبيع الأول (الأدنى) Q1: وهو القيمة التي تقسم مجموعة القراءات (بعد ترتيبها تصاعدياً) إلى قسمين بحيث يسبقها ربع البيانات ويليها ثلاثة أرباع البيانات.
الرُبيع الثاني (الوسيط) Q2: وهو القيمة التي تقسم مجموعة القراءات (بعد ترتيبها تصاعدياً) إلى قسمين بحيث يسبقها نصف البيانات ويليها نصف البيانات أيضاً.
الرُبيع الثالث (الأعلى) Q3: وهو القيمة التي تقسم مجموعة القراءات (بعد ترتيبها تصاعدياً) إلى قسمين بحيث يسبقها ثلاثة أرباع البيانات ويليها ربع البيانات.
ثانياً: مقاييس التشتت المطلق Measures of Dispersion
من أهم مقاييس التشتت المطلق: المدى، نصف المدى الرُبيعي (الانحراف الرُبيعي)، الانحراف المتوسط ، التباين والانحراف المعياري.
(1) المدى Range:
المدى هو أبسط مقاييس التشتت المطلق ويُعرف بأنه الفرق بين أكبر وأصغر قيمة في مجموعة البيانات ويرمز له بالرمز R.
(2) نصف المدى الرُبيعي (الانحراف الربيعي) Quartile Deviation:
يمكن التخلص من العيب الذي يسببه المدى وهو تأثره بالقيم المتطرفة وذلك بأن نستبعد الرُبع الأول من القراءات والرُبع الأخير منها ويُحسب المدى للقراءات الباقية. وتستخدم نصف المسافة بين الرُبيعيين الأدنى والأعلى كمقياس للتشتت في حالة وجود قيم متطرفة ويسمى هذا المقياس بنصف المدى الرُبيعي أو الانحراف الرُبيعي
(3) التباين والانحراف المعياري:
يعتبر التباين من أهم مقاييس التشتت المطلق ويعرف تباين مجموعة من القيم بأنه متوسط مجموع مربعات انحرافات هذه القيم عن وسطها الحسابي وبذلك فإن وحدات التباين هي مربع وحدات البيانات الأصلية. فإذا كانت وحدات القراءات الأصلية بالدينار فتكون وحدات التباين (الدينار)2 وهكذا، ويرمز له بالرمز .
والانحراف المعياري لمجموعة من البيانات هو الجذر التربيعي الموجب للتباين، وبذلك فإن وحدات الانحراف المعياري هي نفس وحدات البيانات الأصلية ويرمز له الرمز S، وغالباً يفضل استخدام الانحراف المعياري لأن مقياس التشتت المطلق يجب أن يكون له نفس وحدات القراءات الأصلية وهو متحقق في حالة الانحراف المعياري.
ثالثاً: الالتواء Skewness
الالتواء هو بعد التوزيع عن التماثل، وقد يكون هذا التوزيع متماثلاً أو ملتوياً جهة اليمين أو ملتوياً جهة اليسار.
ففي حالة التوزيعات المتماثلة فإن الوسط الحسابي = الوسيط = المنوال
إذا كان التوزيع ملتوياً جهة اليمين فإن:
الوسط الحسابي > الوسيط > المنوال
ويسمى توزيع موجب الالتواء وفيه يكون الطرف الأيمن للمنحنى أطول من الأيسر.
إذا كان التوزيع ملتوياً جهة اليسار فإن:
الوسط الحسابي < الوسيط < المنوال
ويسمى توزيع سالب الالتواء وفيه يكون الطرف الأيسر للمنحنى أطول من الأيمن.
معظم قيم مفردات أي ظاهرة لها الرغبة في التجمع أو التمركز حول قيمة معينة تسمى القيمة المتوسطة، هذا التجمع عند هذه القيمة يسمى بالنزعة المركزية للبيانات.
أهم مقاييس النزعة المركزية:
الوسط الحسابي، الوسيط ، المنوال ،الرُبيعات، الوسط الهندسي،الوسط التوافقي.
(1) الوسط الحسابي Arithmetic Mean أو Average
الوسط الحسابي لمجموعة من القيم هو القيمة التي لو أعطيت لكل مفردة من مفردات المجموعة لكان مجموع القيم الجديدة مساويا لمجموع القيم الأصلية ويرمز له بالرمز . وستخدم الوسط الحسابي في حالة البيانات الرقمية فقط.
(2) الوسيط Median:
يعرف الوسيط لمجموعة من البيانات بأنه القيمة التي تقع في وسط المجموعة تماماً بعد ترتبيها تصاعدياً أو تنازلياً، أي هو القيمة التي تقسم مجموعة البيانات إلى قسمين بحيث يكون عدد القيم الأكبر منها مساوياً عدد القيم الأصغر منها ويرمز له بالرمز . ويستخدم الوسيط في حالة البيانات الترتيبية.
(3) المنوال Mode:
يعرف المنوال لمجموعة من البيانات بأنه القيمة الأكثر شيوعاً (تكراراً) في المجموعة ويرمز له بالرمز . يفضل استخدام المنوال في حالة البيانات الوصفية والترتيبية.
4- الرُبيعات Quartiles
يمكن تقسم المساحة تحت المضلع التكراري إلى أربعة أقسام متساوية تسمى الرُبيعات وعددها ثلاثة هي من اليسار إلى اليمين:
الرُبيع الأول (الأدنى) Q1: وهو القيمة التي تقسم مجموعة القراءات (بعد ترتيبها تصاعدياً) إلى قسمين بحيث يسبقها ربع البيانات ويليها ثلاثة أرباع البيانات.
الرُبيع الثاني (الوسيط) Q2: وهو القيمة التي تقسم مجموعة القراءات (بعد ترتيبها تصاعدياً) إلى قسمين بحيث يسبقها نصف البيانات ويليها نصف البيانات أيضاً.
الرُبيع الثالث (الأعلى) Q3: وهو القيمة التي تقسم مجموعة القراءات (بعد ترتيبها تصاعدياً) إلى قسمين بحيث يسبقها ثلاثة أرباع البيانات ويليها ربع البيانات.
ثانياً: مقاييس التشتت المطلق Measures of Dispersion
من أهم مقاييس التشتت المطلق: المدى، نصف المدى الرُبيعي (الانحراف الرُبيعي)، الانحراف المتوسط ، التباين والانحراف المعياري.
(1) المدى Range:
المدى هو أبسط مقاييس التشتت المطلق ويُعرف بأنه الفرق بين أكبر وأصغر قيمة في مجموعة البيانات ويرمز له بالرمز R.
(2) نصف المدى الرُبيعي (الانحراف الربيعي) Quartile Deviation:
يمكن التخلص من العيب الذي يسببه المدى وهو تأثره بالقيم المتطرفة وذلك بأن نستبعد الرُبع الأول من القراءات والرُبع الأخير منها ويُحسب المدى للقراءات الباقية. وتستخدم نصف المسافة بين الرُبيعيين الأدنى والأعلى كمقياس للتشتت في حالة وجود قيم متطرفة ويسمى هذا المقياس بنصف المدى الرُبيعي أو الانحراف الرُبيعي
(3) التباين والانحراف المعياري:
يعتبر التباين من أهم مقاييس التشتت المطلق ويعرف تباين مجموعة من القيم بأنه متوسط مجموع مربعات انحرافات هذه القيم عن وسطها الحسابي وبذلك فإن وحدات التباين هي مربع وحدات البيانات الأصلية. فإذا كانت وحدات القراءات الأصلية بالدينار فتكون وحدات التباين (الدينار)2 وهكذا، ويرمز له بالرمز .
والانحراف المعياري لمجموعة من البيانات هو الجذر التربيعي الموجب للتباين، وبذلك فإن وحدات الانحراف المعياري هي نفس وحدات البيانات الأصلية ويرمز له الرمز S، وغالباً يفضل استخدام الانحراف المعياري لأن مقياس التشتت المطلق يجب أن يكون له نفس وحدات القراءات الأصلية وهو متحقق في حالة الانحراف المعياري.
ثالثاً: الالتواء Skewness
الالتواء هو بعد التوزيع عن التماثل، وقد يكون هذا التوزيع متماثلاً أو ملتوياً جهة اليمين أو ملتوياً جهة اليسار.
ففي حالة التوزيعات المتماثلة فإن الوسط الحسابي = الوسيط = المنوال
إذا كان التوزيع ملتوياً جهة اليمين فإن:
الوسط الحسابي > الوسيط > المنوال
ويسمى توزيع موجب الالتواء وفيه يكون الطرف الأيمن للمنحنى أطول من الأيسر.
إذا كان التوزيع ملتوياً جهة اليسار فإن:
الوسط الحسابي < الوسيط < المنوال
ويسمى توزيع سالب الالتواء وفيه يكون الطرف الأيسر للمنحنى أطول من الأيمن.
تشغيل والتعرف على البرنامج SPSS
يعمل البرنامج الإحصائي SPSS في بيئة النوافذ، ويتم تشغيله باختيار الأمر Start من اللائحة الرئيسة Programs وبعد ذلك حدد برنامج SPSS.
نوافذ البرنامج
هناك عدة نوافذ للبرنامج نذكر منها ما يلي:
1ـ لائحة الأوامر Command Functions.
2ـ شاشة البيانات Data View.
3ـ شاشة تعريف المتغيرات variable view.
4ـ لائحة التقارير والمخرجات Output Navigator.
1- لائحة الأوامر
وهو الجزء الخاص بالأوامر، حيث يمكن اختيار الأمر من خلال ICON لكل عملية إحصائية وتعرض النتائج في لائحة التقارير، وتشمل اللائحة على 9 أوامر رئيسة ( بدون Help) يتفرع منها عدد من الأوامر الفرعية.
2- لائحة البيانات
لإضافة وإلغاء البيانات التابعة لكل متغير، حيث يتم تمثيل المتغير بعمود Column ويعطي الاسم VAR مع رقم يبدأ من 1 حتى 100,000، أما الأسطر فتمثل عدد المشاهدات لكل متغير. ويتم التحويل ما بين المشاهدات والمتغيرات بالضغط على Data View و Variable View.
3- شاشة تعريف المتغيرات
لتعريف المتغيرات يتم الضغط على العمود مرتين Double Click او بالضغط على Variable View الموجود في أسفل الشاشة لتظهر شاشة أخرى لتعريف المتغيرات بتحديد اسم المتغير النوع، الحجم، العنوان، الترميز. ويتم الترميز بالضغط على عامود Values ومن ثم تحديد قيمة الرمز ووصفه مع الضغط على مفتاح ADD لإضافة الرمز.
4- لائحة التقارير والنتائج:
شاشة لإظهار النتائج والتقارير، ويتم التحويل ما بين شاشة النتائج وشاشة البيانات بالضغط على الأمر Window ومن ثم اختيار ملف البيانات.
استرجاع البيانات والملفات:
باختيار الأمر File ثم الفرعي Open، لا بد بعد ذلك من تحديد نوعية الملف المراد استرجاعه.
ويتم استرجاع التالي:
بيانات ( المتغيرات ) (*. Sav).
تقارير، والمقصود بتقارير نتائج العمليات الإحصائية التي تم عملها سابقاً (*.Spo).
وذلك بعد اختيار اسم الملف المطلوب مع التأكيد على مفتاح Open. وكذلك يمكن استرجاع ملفات الاكسيل (*.xls) وأنواع ملفات أخرى.
حفظ الملف:
الأمر الفرعي Save و Save as خاصان لحفظ البيانات، حيث
1) Save As يستخدم لإعطاء اسم جديد للملف مع حفظه ويمكن كما ذكر سابقاً حفظ ما يلي:
- بيان المتغيرات “Data”
- تقارير “Output Navigator”
2) Save لحفظ التعديلات الجديدة التي طرأت على الملف.
إضافة، تعديل والتحكم بالمتغيرات
انتقل إلى نافذة Data Editor واختر متغير غير محجوز (عمود) وأضف البيانات مع التأكيد على مفتاح Enter أو تحرير السهم إلى أسفل (ملاحظة: . تعني Missing أي لا توجد قيمة في هذه الخلية).
تعديل البيانات:
ويمكن بسهولة تعديل أي قيمة وذلك بتحريك السهم إلى الصف ( الخلية) والكتابة عليها بالقيمة الجديدة.
تعريف المتغيرات:
يمكن تحديد نوعية البيانات المضافة فالمتغيرات والمؤشرات الاقتصادية يمكن إضافتها كما هي، أما المتغيرات والبيانات تحدد من قبل الباحث بطريقة البدائل ( ذكر أو أنثى، متعلم أو غير متعلم) ويتم تعريف المتغير بالانتقال إلى شاشة تعريف المتغيرات Variable View وتحديد الآتي:
اسم المتغير، النوع، حجم المتغير، عدد النقاط العشرية.
تحديد قيم المتغير ( الترميز ) في خانة Values.
إدخال قيمة الرمز في خانة Value واسم الرمز في خانة Value Label والضغط على مفتاح ADD في كل مرة.
بعد إجراء الخطوات السابقة يتم إضافة المتغيرات في شاشة البيانات ولإظهار القيم الكتابية المرادفة بدل القيم الرقمية وذلك بإجراء ما يلي:
اختر الأمر View من اللائحة الرئيسة.
اختر الأمر الفرعي Value Labels أو الضغط على المفتاح .
أنظر المربع الحواري التالي مثلاً:
مثال:
في حالة وجود أكثر من متغير بنفس عناوين قيم البيانات ، وتكون الاختيارات: موافق بشدة، موافق، متردد، غير موافق، غير موافق على الإطلاق وبفرض أنه يوجد 10 متغيرات في مثل هذه الحالة، ولتنفيذ ذلك يمكن إتباع الخطوات التالية:
1- يتم تعريف الاختيارات السابقة كما تم شرحه في تعريف قيم المتغيرات.
2- نسخ المتغير السابق تعريفه، (Edit, copy) أو ctrl + c
3- اختر الصف التالي للمتغير السابق بالفأرة ثم اضغط على المفتاح الأيمن للفأرة، من القائمة المنسدلة يتم اختيار Paste variables… كما في الشكل التالي.
4- يظهر المربع الحواري التالي:
5- أكمل المربع الحواري السابق كما يلي:
6- اختر OK فنحصل على المطلوب كما في الشكل التالي:
إضافة متغير أو مشاهدة:
يمكن إضافة مشاهدة أو متغير جديد وذلك باستعمال الأمر الرئيسي DATA ثم:
الأمر الفرعي Insert Variable في حالة إضافة متغير جديد أو الضغط على مفتاح .
الأمر الفرعي Insert Case في حالة إضافة مشاهدة جديدة أو الضغط على مفتاح .
الأمر الفرعي Sort Cases لترتيب البيانات حسب المتغير المراد الترتيب به.
الأمر الفرعي Goto Case لتحويل المؤشر إلى مشاهدة معينة أو الضغط على مفتاح .
ولعرض المتغيرات المستخدمة قيد الدراسة يتم الضغط على مفتاح أو باستخدام الأمر الرئيسي Utilities ثم الأمر الفرعي Variables.
إلغاء متغير أو مشاهدة أو حالة
ضع المؤشر في مكان المتغير المراد إلغاؤه ثم اضغط على مفتاح Del، وفي حالة إلغاء مشاهدة ضع المؤشر على مكان الخلية ( المشاهدة ) ثم اضغط على مفتاح Del. ولإلغاء حالة معينة يجب أن تضغط بالفأرة على تلك الحالة ثم اضغط على مفتاح Del.
ترتيب المشاهدات حسب متغير معين Rank Cases
يقوم برنامج SPSS بانشاء متغير جديد يحتوي على الرقم التسلسلي لترتيب المشاهدات إما تصاعدياً أو تنازلياً، وذلك باختيار الأمر الفرعي Rank Cases من الأمر الرئيسي Transform.
نوافذ البرنامج
هناك عدة نوافذ للبرنامج نذكر منها ما يلي:
1ـ لائحة الأوامر Command Functions.
2ـ شاشة البيانات Data View.
3ـ شاشة تعريف المتغيرات variable view.
4ـ لائحة التقارير والمخرجات Output Navigator.
1- لائحة الأوامر
وهو الجزء الخاص بالأوامر، حيث يمكن اختيار الأمر من خلال ICON لكل عملية إحصائية وتعرض النتائج في لائحة التقارير، وتشمل اللائحة على 9 أوامر رئيسة ( بدون Help) يتفرع منها عدد من الأوامر الفرعية.
2- لائحة البيانات
لإضافة وإلغاء البيانات التابعة لكل متغير، حيث يتم تمثيل المتغير بعمود Column ويعطي الاسم VAR مع رقم يبدأ من 1 حتى 100,000، أما الأسطر فتمثل عدد المشاهدات لكل متغير. ويتم التحويل ما بين المشاهدات والمتغيرات بالضغط على Data View و Variable View.
3- شاشة تعريف المتغيرات
لتعريف المتغيرات يتم الضغط على العمود مرتين Double Click او بالضغط على Variable View الموجود في أسفل الشاشة لتظهر شاشة أخرى لتعريف المتغيرات بتحديد اسم المتغير النوع، الحجم، العنوان، الترميز. ويتم الترميز بالضغط على عامود Values ومن ثم تحديد قيمة الرمز ووصفه مع الضغط على مفتاح ADD لإضافة الرمز.
4- لائحة التقارير والنتائج:
شاشة لإظهار النتائج والتقارير، ويتم التحويل ما بين شاشة النتائج وشاشة البيانات بالضغط على الأمر Window ومن ثم اختيار ملف البيانات.
استرجاع البيانات والملفات:
باختيار الأمر File ثم الفرعي Open، لا بد بعد ذلك من تحديد نوعية الملف المراد استرجاعه.
ويتم استرجاع التالي:
بيانات ( المتغيرات ) (*. Sav).
تقارير، والمقصود بتقارير نتائج العمليات الإحصائية التي تم عملها سابقاً (*.Spo).
وذلك بعد اختيار اسم الملف المطلوب مع التأكيد على مفتاح Open. وكذلك يمكن استرجاع ملفات الاكسيل (*.xls) وأنواع ملفات أخرى.
حفظ الملف:
الأمر الفرعي Save و Save as خاصان لحفظ البيانات، حيث
1) Save As يستخدم لإعطاء اسم جديد للملف مع حفظه ويمكن كما ذكر سابقاً حفظ ما يلي:
- بيان المتغيرات “Data”
- تقارير “Output Navigator”
2) Save لحفظ التعديلات الجديدة التي طرأت على الملف.
إضافة، تعديل والتحكم بالمتغيرات
انتقل إلى نافذة Data Editor واختر متغير غير محجوز (عمود) وأضف البيانات مع التأكيد على مفتاح Enter أو تحرير السهم إلى أسفل (ملاحظة: . تعني Missing أي لا توجد قيمة في هذه الخلية).
تعديل البيانات:
ويمكن بسهولة تعديل أي قيمة وذلك بتحريك السهم إلى الصف ( الخلية) والكتابة عليها بالقيمة الجديدة.
تعريف المتغيرات:
يمكن تحديد نوعية البيانات المضافة فالمتغيرات والمؤشرات الاقتصادية يمكن إضافتها كما هي، أما المتغيرات والبيانات تحدد من قبل الباحث بطريقة البدائل ( ذكر أو أنثى، متعلم أو غير متعلم) ويتم تعريف المتغير بالانتقال إلى شاشة تعريف المتغيرات Variable View وتحديد الآتي:
اسم المتغير، النوع، حجم المتغير، عدد النقاط العشرية.
تحديد قيم المتغير ( الترميز ) في خانة Values.
إدخال قيمة الرمز في خانة Value واسم الرمز في خانة Value Label والضغط على مفتاح ADD في كل مرة.
بعد إجراء الخطوات السابقة يتم إضافة المتغيرات في شاشة البيانات ولإظهار القيم الكتابية المرادفة بدل القيم الرقمية وذلك بإجراء ما يلي:
اختر الأمر View من اللائحة الرئيسة.
اختر الأمر الفرعي Value Labels أو الضغط على المفتاح .
أنظر المربع الحواري التالي مثلاً:
مثال:
في حالة وجود أكثر من متغير بنفس عناوين قيم البيانات ، وتكون الاختيارات: موافق بشدة، موافق، متردد، غير موافق، غير موافق على الإطلاق وبفرض أنه يوجد 10 متغيرات في مثل هذه الحالة، ولتنفيذ ذلك يمكن إتباع الخطوات التالية:
1- يتم تعريف الاختيارات السابقة كما تم شرحه في تعريف قيم المتغيرات.
2- نسخ المتغير السابق تعريفه، (Edit, copy) أو ctrl + c
3- اختر الصف التالي للمتغير السابق بالفأرة ثم اضغط على المفتاح الأيمن للفأرة، من القائمة المنسدلة يتم اختيار Paste variables… كما في الشكل التالي.
4- يظهر المربع الحواري التالي:
5- أكمل المربع الحواري السابق كما يلي:
6- اختر OK فنحصل على المطلوب كما في الشكل التالي:
إضافة متغير أو مشاهدة:
يمكن إضافة مشاهدة أو متغير جديد وذلك باستعمال الأمر الرئيسي DATA ثم:
الأمر الفرعي Insert Variable في حالة إضافة متغير جديد أو الضغط على مفتاح .
الأمر الفرعي Insert Case في حالة إضافة مشاهدة جديدة أو الضغط على مفتاح .
الأمر الفرعي Sort Cases لترتيب البيانات حسب المتغير المراد الترتيب به.
الأمر الفرعي Goto Case لتحويل المؤشر إلى مشاهدة معينة أو الضغط على مفتاح .
ولعرض المتغيرات المستخدمة قيد الدراسة يتم الضغط على مفتاح أو باستخدام الأمر الرئيسي Utilities ثم الأمر الفرعي Variables.
إلغاء متغير أو مشاهدة أو حالة
ضع المؤشر في مكان المتغير المراد إلغاؤه ثم اضغط على مفتاح Del، وفي حالة إلغاء مشاهدة ضع المؤشر على مكان الخلية ( المشاهدة ) ثم اضغط على مفتاح Del. ولإلغاء حالة معينة يجب أن تضغط بالفأرة على تلك الحالة ثم اضغط على مفتاح Del.
ترتيب المشاهدات حسب متغير معين Rank Cases
يقوم برنامج SPSS بانشاء متغير جديد يحتوي على الرقم التسلسلي لترتيب المشاهدات إما تصاعدياً أو تنازلياً، وذلك باختيار الأمر الفرعي Rank Cases من الأمر الرئيسي Transform.
تكوين متغير جديد باستخدام معادلة
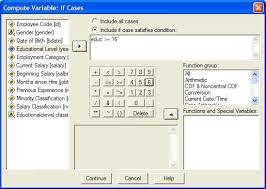
أختر من اللائحة الرئيسة الأمر Transform، ثم الأمر الفرعي Compute بعد ذلك حدد اسم المتغير الجديد في Target Variable ثم كتابة المعادلة التي سوف تقوم بتكوينها باستخدام المتغيرات المعرفة مسبقاً. وبالضغط على مفتاح لتحديد شرط تحقيق المعادلة. أنظر المربع الحواري التالي:
استخدام الدالة IF مع Compute
تستخدم الدالة IF في حالة إضافة شرط معين لحساب قيم متغير جديد بالنسبة لمتغير موجود مسبقاً
فمثلاَ: افتح الملف Employee Data.
المطلوب: إعطاء مكافأة مقدارها مرتب شهر واحد للموظفين الذين تعلموا 16 سنة فأكثر.
SPSS STEP BY STEP
Transform Compute
توجد عدة اختيارات في المربع الحواري السابق هي:
1ـ All cases
يستخدم هذا الاختيار في حالة استخدام جميع الخلايا دون تحقيق شرط معين وهذا هو الاختيار المبدئي في SPSS.
2. If condition is satisfied
يستخدم هذا الاختيار في حالة اختيار بعض الخلايا التي تحقق شرط معين، ويمكن استخدام الرموز التالية مع هذا الاختيار:
يمكن استخدام الرموز المنطقية التالية مع الدالة If: and " & "، or " | "
ولتنفيذ ذلك نشط هذا الاختيار ثم اضغط If فيظهر المربع الحواري التالي:
فمثلاً:
لاختيار الحالات التي أقل من 18 سنة مثلاً لقيم المتغير educنستخدم علامة أقل من " < " يمكن استخدام الشرط التالي:
educ < 18 أو educ <= 17
لاختيار الموظفين بدون المدراء فقط يمكن استخدام العلامة لا يساوي " ~= " حيث تم تصنيف المدراء بالرقم 3 لتنفيذ ذلك استخدام الشرط التالي:
Jobcat ~= 3
لاختيار الموظفين الذكور الذين تعلموا أكثر من 18 سنة ومدراء يمكن استخدام الشرط التالي:
Gender = “m” & educ >18 & jobcat = 3
علماً بأن المتغير Gender متغير وصفي تم تصنيفه إلى نوعين هما: m: ذكور، f: إناث، وفي حالة المتغير الوصفي يجب وضع الرمز المناسب (m, f) بين علامتي تنصيص " ".
لاختيار الموظف الذي يعمل في وظيفة كاتب أو مدير يمكن استخدام الشرط التالي:
Jobcat = 1 | Jobcat = 3
مع ملاحظة أنه من الضروري تكرار اسم المتغير، أي أنه من الخطأ استخدام الشرط السابق على النحو التالي:
Jobcat = 1 | 3
يمكن استخدام دالة any لاختيار الموظف الذي يعمل في وظيفة كاتب أو مدير كما يلي:
any( Jobcat, 1 , 3 )
لاختيار الموظفين الذين تعلموا بين 18 سنة و 20 سنة مثلاً يمكن استخدام الشرط التالي:
educ >=18 & educ <= 20
أو يمكن استخدام الشرط في الصورة التالية:
range (educ,18,20)
3. Random sample of cases
يستخدم هذا الاختيار في حالة اختيار عينة عشوائية بحجم معين، ولتنفيذ ذلك نشط هذا الاختيار ثم اضغط Sample فيظهر المربع الحواري التالي:
يوجد اختياران في المربع الحواري السابق هما:
Approximately: يستخدم لاختيار نسبة مئوية تقريبية من الحالات، فمثلاً يمكن اختيار 20% تقريباً من كل الخلايا.
Exactly: يستخدم لاختيار عينة عشوائية ذات حجم معين من أول عدد مناسب من الخلايا مع ملاحظة أن عدد الخلايا المطلوب اختيارها يجب أن يكون أقل من عدد الخلايا المطلوب الاختيار منها، فمثلاً يمكن اختيار 100 خلية فقط من أول 150 خلية.
4. Based on time or case range
يستخدم هذا الاختيار في حالة اختيار عينة عشوائية بحجم معين، ولتنفيذ ذلك نشط هذا الاختيار ثم اضغط
Range فيظهر المربع الحواري التالي:
لاختيار الحالات بين 20، 50 مثلاً اكتب في المربع الحواري السابق اكتب 20 في المستطيل أسفل First Case، 50 في المستطيل أسفل Last Case.
5. Use filter variable
يستخدم هذا الاختيار في حالة استخدام متغير رقمي كمتغير لتصفية الخلايا المطلوبة، وفي هذه الحالة فإن الخلايا التي قيمها لا تساوي صفراً أو ليست قيم مفقودة لمتغير التصفية سوف يتم اختيارها.
الاختيار Filtered أسفل Unselected Cases Are: يستخدم لتصفية الخلايا الغير مطلوبة مع إبقائها في ملف البيانات، أما الاختيار Deleted فيستخدم لمسح الخلايا الغير مطلوبة من ملف البيانات.
إعادة الترميز Recode
يستخدم الأمر Recode في عمليات الفرز لمجموعات مختلفة، وذلك بهدف إنشاء جداول تكرارية مختصرة ويمكن تنفيذ ذلك على نفس المتغير أو إنشاء متغير جديد وينصح بإنشاء متغير جديد لأن تنفيذ الأمر Recode على نفس المتغير يعمل على مسح قيم المتغير الأصلية التي قد تستخدم فيما بعد لأغراض تحليلية أخرى.
المطلوب: فرز عدد سنوات التعليم (educ) في ملف Employee data وذلك في متغير جديد باسم educ_new حسب التصنيف التالي:
1ـ All cases
يستخدم هذا الاختيار في حالة استخدام جميع الخلايا دون تحقيق شرط معين وهذا هو الاختيار المبدئي في SPSS.
2. If condition is satisfied
يستخدم هذا الاختيار في حالة اختيار بعض الخلايا التي تحقق شرط معين، ويمكن استخدام الرموز التالية مع هذا الاختيار:
< | أصغر من | <= | أصغر من أو يساوي |
> | أكبر من | >= | أكبر من أو يساوي |
= | يساوي | ~= | لا يساوي |
ولتنفيذ ذلك نشط هذا الاختيار ثم اضغط If فيظهر المربع الحواري التالي:
فمثلاً:
لاختيار الحالات التي أقل من 18 سنة مثلاً لقيم المتغير educنستخدم علامة أقل من " < " يمكن استخدام الشرط التالي:
educ < 18 أو educ <= 17
لاختيار الموظفين بدون المدراء فقط يمكن استخدام العلامة لا يساوي " ~= " حيث تم تصنيف المدراء بالرقم 3 لتنفيذ ذلك استخدام الشرط التالي:
Jobcat ~= 3
لاختيار الموظفين الذكور الذين تعلموا أكثر من 18 سنة ومدراء يمكن استخدام الشرط التالي:
Gender = “m” & educ >18 & jobcat = 3
علماً بأن المتغير Gender متغير وصفي تم تصنيفه إلى نوعين هما: m: ذكور، f: إناث، وفي حالة المتغير الوصفي يجب وضع الرمز المناسب (m, f) بين علامتي تنصيص " ".
لاختيار الموظف الذي يعمل في وظيفة كاتب أو مدير يمكن استخدام الشرط التالي:
Jobcat = 1 | Jobcat = 3
مع ملاحظة أنه من الضروري تكرار اسم المتغير، أي أنه من الخطأ استخدام الشرط السابق على النحو التالي:
Jobcat = 1 | 3
يمكن استخدام دالة any لاختيار الموظف الذي يعمل في وظيفة كاتب أو مدير كما يلي:
any( Jobcat, 1 , 3 )
لاختيار الموظفين الذين تعلموا بين 18 سنة و 20 سنة مثلاً يمكن استخدام الشرط التالي:
educ >=18 & educ <= 20
أو يمكن استخدام الشرط في الصورة التالية:
range (educ,18,20)
3. Random sample of cases
يستخدم هذا الاختيار في حالة اختيار عينة عشوائية بحجم معين، ولتنفيذ ذلك نشط هذا الاختيار ثم اضغط Sample فيظهر المربع الحواري التالي:
يوجد اختياران في المربع الحواري السابق هما:
Approximately: يستخدم لاختيار نسبة مئوية تقريبية من الحالات، فمثلاً يمكن اختيار 20% تقريباً من كل الخلايا.
Exactly: يستخدم لاختيار عينة عشوائية ذات حجم معين من أول عدد مناسب من الخلايا مع ملاحظة أن عدد الخلايا المطلوب اختيارها يجب أن يكون أقل من عدد الخلايا المطلوب الاختيار منها، فمثلاً يمكن اختيار 100 خلية فقط من أول 150 خلية.
4. Based on time or case range
يستخدم هذا الاختيار في حالة اختيار عينة عشوائية بحجم معين، ولتنفيذ ذلك نشط هذا الاختيار ثم اضغط
Range فيظهر المربع الحواري التالي:
لاختيار الحالات بين 20، 50 مثلاً اكتب في المربع الحواري السابق اكتب 20 في المستطيل أسفل First Case، 50 في المستطيل أسفل Last Case.
5. Use filter variable
يستخدم هذا الاختيار في حالة استخدام متغير رقمي كمتغير لتصفية الخلايا المطلوبة، وفي هذه الحالة فإن الخلايا التي قيمها لا تساوي صفراً أو ليست قيم مفقودة لمتغير التصفية سوف يتم اختيارها.
الاختيار Filtered أسفل Unselected Cases Are: يستخدم لتصفية الخلايا الغير مطلوبة مع إبقائها في ملف البيانات، أما الاختيار Deleted فيستخدم لمسح الخلايا الغير مطلوبة من ملف البيانات.
إعادة الترميز Recode
يستخدم الأمر Recode في عمليات الفرز لمجموعات مختلفة، وذلك بهدف إنشاء جداول تكرارية مختصرة ويمكن تنفيذ ذلك على نفس المتغير أو إنشاء متغير جديد وينصح بإنشاء متغير جديد لأن تنفيذ الأمر Recode على نفس المتغير يعمل على مسح قيم المتغير الأصلية التي قد تستخدم فيما بعد لأغراض تحليلية أخرى.
المطلوب: فرز عدد سنوات التعليم (educ) في ملف Employee data وذلك في متغير جديد باسم educ_new حسب التصنيف التالي:
الإحصاء الوصفي والمدرج التكراري للبيانات
(1) التكرارات والمدرج التكراري Histogram and Frequencies
اختر من اللائحة الرئيسة ما يلي:
Analyze
اختر الأمر Descriptive Statistics.
Frequencies وتستخدم لعرض الجداول التكرارية للمتغيرات موضع الدراسة
(2) الإحصاء الوصفي Descriptive Statistics
اختر من اللائحة الرئيسة ما يلي:
1- ANALYZE
2- اختر من الأمر DESCRIPTIVE STATISTICS
3- DESCRIPTIVES وتعني الإحصاء الوصفي
ولتحديد مخرجات الإحصاء الوصفي اختر Option من اللائحة الفرعية، ثم حدد ما هو المطلوب.
(3) المستكشف Explore
اختر من اللائحة الرئيسة ما يلي:
1- ANALYZE
2- اختر الأمر DESCRIPTIVE STATISTICS
3- EXPLORE وتعني إظهار الخصائص الإحصائية للمتغير- جميع المتغيرات كل على حدة أو حسب مجموعات ذات خصائص معينة. وذلك بكتابة المتغير "المراد إظهار صفاته الإحصائية" في خانة DEPENDENT LIST ولتحديد المجموعة يتم كتابة المتغير في خانة FACTOR LIST.
(4) جداول الاقتران CROSS TABULATION
اختر من اللائحة الرئيسة ما يلي:
1- ANALYZE ثم اختر الأمر DESCRIPTIVE STATISTICS.
2- CROSSTABS، تستخدم إحصائية CHI-SQAURE في جداول الاقتران لمعرفة مدى استقلالية المتغيرات عن بعضها البعض.
اختر من اللائحة الرئيسة ما يلي:
Analyze
اختر الأمر Descriptive Statistics.
Frequencies وتستخدم لعرض الجداول التكرارية للمتغيرات موضع الدراسة
(2) الإحصاء الوصفي Descriptive Statistics
اختر من اللائحة الرئيسة ما يلي:
1- ANALYZE
2- اختر من الأمر DESCRIPTIVE STATISTICS
3- DESCRIPTIVES وتعني الإحصاء الوصفي
ولتحديد مخرجات الإحصاء الوصفي اختر Option من اللائحة الفرعية، ثم حدد ما هو المطلوب.
(3) المستكشف Explore
اختر من اللائحة الرئيسة ما يلي:
1- ANALYZE
2- اختر الأمر DESCRIPTIVE STATISTICS
3- EXPLORE وتعني إظهار الخصائص الإحصائية للمتغير- جميع المتغيرات كل على حدة أو حسب مجموعات ذات خصائص معينة. وذلك بكتابة المتغير "المراد إظهار صفاته الإحصائية" في خانة DEPENDENT LIST ولتحديد المجموعة يتم كتابة المتغير في خانة FACTOR LIST.
(4) جداول الاقتران CROSS TABULATION
اختر من اللائحة الرئيسة ما يلي:
1- ANALYZE ثم اختر الأمر DESCRIPTIVE STATISTICS.
2- CROSSTABS، تستخدم إحصائية CHI-SQAURE في جداول الاقتران لمعرفة مدى استقلالية المتغيرات عن بعضها البعض.
اختبار الفرضيات Test of Hypotheses
يعتبر موضوع اختبار الفرضيات الإحصائية من أهم الموضوعات في مجال اتخاذ القرارات وسنبدأ بذكر بعض المصطلحات الهامة في هذا المجال.
1- الفرضية الإحصائية
هي عبارة عن ادعاء قد يكون صحيحاً أو خطأ حول معلمة أو أكثر لمجتمع أو لمجموعة من المجتمعات.
تقبل الفرضية في حالة أن بيانات العينة تساند النظرية، وترفض عندما تكون بيانات العينة على النقيض منها، وفي حالة عدم رفضنا للفرضية الإحصائية فإن هذا ناتج عن عدم وجود أدلة كافية لرفضها من بيانات العينة ولذلك فإن عدم رفضنا لهذه الفرضية لا يعنى بالضرورة أنها صحيحة، أما إذا رفضنا الفرضية بناء على المعلومات الموجودة في بيانات العينة فهذا يعنى أن الفرضية خاطئة، ولذلك فإن الباحث يحاول أن يضع الفرضية بشكل يأمل أن يرفضها، فمثلاً إذا أراد الباحث أن يثبت بأن طريقة جديدة من طرق التدريس أحسن من غيرها فإنه يضع فرضية تقول بعدم وجود فرق بين طرق التدريس.
إن الفرضية التي يأمل الباحث أن يرفضها تسمى بفرضية العدم (الفرضية المبدئية) ويرمز لها بالرمز ، ورفضنا لهذه الفرضية يؤدى إلى قبول فرضية بديلة عنها تسمى الفرضية البديلة ويرمز لها بالرمز .
2- مستوى المعنوية أو مستوى الاحتمال
وهي درجة الاحتمال الذي نرفض به فرضية العدم عندما تكون صحيحة أو هو احتمال الوقوع في الخطأ من النوع الأول ويرمز له بالرمز، وهي يحددها الباحث لنفسه منذ البداية وفي معظم العلوم التطبيقية نختار مساوية 1% أو 5 % على الأكثر.
3- دالة الاختبار الإحصائية
عبارة عن متغير عشوائي له توزيع احتمالي معلوم وتصف الدالة الإحصائية العلاقة بين القيم النظرية للمجتمع والقيم المحسوبة من العينة.
4- القيمة الاحتمالية (Sig. or P-value) :
احتمال الحصول على قيمة أكبر من أو تساوي (أقل من أو تساوي) إحصائية الاختبار المحسوبة من بيانات العينة أخذاً في الاعتبار توزيع إحصائية الاختبار بافتراض صحة فرض العدم وطبيعة الفرض البديل . ويتم استخدام القيمة الاحتمالية لاتخاذ قرار حيال فرض العدم.
1- الفرضية الإحصائية
هي عبارة عن ادعاء قد يكون صحيحاً أو خطأ حول معلمة أو أكثر لمجتمع أو لمجموعة من المجتمعات.
تقبل الفرضية في حالة أن بيانات العينة تساند النظرية، وترفض عندما تكون بيانات العينة على النقيض منها، وفي حالة عدم رفضنا للفرضية الإحصائية فإن هذا ناتج عن عدم وجود أدلة كافية لرفضها من بيانات العينة ولذلك فإن عدم رفضنا لهذه الفرضية لا يعنى بالضرورة أنها صحيحة، أما إذا رفضنا الفرضية بناء على المعلومات الموجودة في بيانات العينة فهذا يعنى أن الفرضية خاطئة، ولذلك فإن الباحث يحاول أن يضع الفرضية بشكل يأمل أن يرفضها، فمثلاً إذا أراد الباحث أن يثبت بأن طريقة جديدة من طرق التدريس أحسن من غيرها فإنه يضع فرضية تقول بعدم وجود فرق بين طرق التدريس.
إن الفرضية التي يأمل الباحث أن يرفضها تسمى بفرضية العدم (الفرضية المبدئية) ويرمز لها بالرمز ، ورفضنا لهذه الفرضية يؤدى إلى قبول فرضية بديلة عنها تسمى الفرضية البديلة ويرمز لها بالرمز .
2- مستوى المعنوية أو مستوى الاحتمال
وهي درجة الاحتمال الذي نرفض به فرضية العدم عندما تكون صحيحة أو هو احتمال الوقوع في الخطأ من النوع الأول ويرمز له بالرمز، وهي يحددها الباحث لنفسه منذ البداية وفي معظم العلوم التطبيقية نختار مساوية 1% أو 5 % على الأكثر.
3- دالة الاختبار الإحصائية
عبارة عن متغير عشوائي له توزيع احتمالي معلوم وتصف الدالة الإحصائية العلاقة بين القيم النظرية للمجتمع والقيم المحسوبة من العينة.
4- القيمة الاحتمالية (Sig. or P-value) :
احتمال الحصول على قيمة أكبر من أو تساوي (أقل من أو تساوي) إحصائية الاختبار المحسوبة من بيانات العينة أخذاً في الاعتبار توزيع إحصائية الاختبار بافتراض صحة فرض العدم وطبيعة الفرض البديل . ويتم استخدام القيمة الاحتمالية لاتخاذ قرار حيال فرض العدم.
خطوات اختبار الفرضيات
(1) تحديد نوع توزيع المجتمع
يجب تحديد ما إذا كان المتغير العشوائي الذي يتم دراسته يتبع التوزيع الطبيعي أم توزيع بواسون أم توزيع ذو الحدين أم غيره من التوزيعات الاحتمالية المتصلة أو المنفصلة، معظم التوزيعات الاحتمالية يكون توزيعها مشابهاً للتوزيع الطبيعي خاصة إذا كان حجم العينة كبيراً.
هناك نوعان من الطرق الإحصائية التي تستخدم في اختبار الفرضيات:
( أ ) الاختبارات المعلمية: وتستخدم في حالة البيانات الرقمية التي توزيعها يتبع التوزيع الطبيعي.
(ب) الاختبارات غير المعلمية: وتستخدم في حالة البيانات الرقمية التي توزيعها لا يتبع التوزيع الطبيعي طبيعي، وكذلك في حالتي البيانات الترتيبية والوصفية.
2- صياغة فرضيتا العدم والبديلة
مثلاً: عند اختبار أن متوسط المجتمع يساوى قيمة معينة مقابل الفرضية القائلة بأن لا يساوى ، فإن فرضية العدم والفرضية البديلة تكون على النحو التالي:
3- اختيار مستوى المعنوية
4- اختيار دالة الاختبار الإحصائية المناسبة
5- جمع البيانات من العينة وحساب قيمة دالة الاختبار الإحصائية
6- اتخاذ القرارات
نرفض ونقبلإذا كانت قيمة الاحتمال (Sig. or P-value) أقل من أو تساوي مستوى المعنوية ()، أما إذا كانت قيمة الاحتمال أكبر من فلا يمكن رفض .
وبرنامج SPSS يعطي Sig. 2-tailed فبالتالي نرفض فرضية العدم عندما تكون .
أولاً: اختبار T في حالة اختبار فرضيات متعلقة بمتوسط واحد
إذا كان المطلوب اختبار فرضية العدم على مستوى دلالة مقابل
مثال (1)
البيانات التالية تمثل درجات عشرين طالباً في مساق ما:
65, 72, 68, 82, 45, 92, 87, 85, 90, 60, 48, 60, 68, 72, 79, 68, 73, 69, 78, 84
المطلوب: اختبار الفرضية المبدئية القائلة بأن متوسط درجات الطلاب = 65 درجة.
SPSS STEP BY STEP
Analyze Compare Means One-Sample T Test
ثانياً: اختبارات الفروق بين متوسطين مجتمعين مستقلين
في هذه الحالة نأخذ عينة عشوائية من توزيع طبيعي ، وعينة عشوائية أيضاً من توزيع طبيعي ومستقل عن التوزيع الأول، وتكون ولكنهما مجهولتان.
إذا كان المطلوب اختبار فرضية العدم على مستوى دلالة مقابل
مثال (2)
مستخدماً الملف employee. المطلوب اختبار ما إذا كان هناك فرق معنوي بين متوسط الراتب الحالي السنوي للموظفين (salary) يعزى إلى متغير الجنس (gender) مستخدماً مستوى معنوية.
SPSS STEP BY STEP
Analyze Compare Means Independent- Samples T Test
ثالثاً: اختبارات الفروق بين متوسطي مجتمعين من عينات مرتبطة
في هذه الحالة تكون البيانات مزدوجة، أي أن العينتين مرتبطتان حيث أن البيانات تكون على شكل أزواج وبالتالي فإن حجم العينتين لابد أن يكون متساوياً.
مثال (3)
البيانات التالية تمثل نتائج تجربة أجريت على عشرين شخصاً لاختبار مدى فعالية نظام خاص من الغذاء لتخفيف الوزن، حيث تم قياس أوزانهم قبل البدء في تطبيق هذا النظام، وبعد اتباع هذا النظام الخاص لمدة ثلاثة شهور.
يجب تحديد ما إذا كان المتغير العشوائي الذي يتم دراسته يتبع التوزيع الطبيعي أم توزيع بواسون أم توزيع ذو الحدين أم غيره من التوزيعات الاحتمالية المتصلة أو المنفصلة، معظم التوزيعات الاحتمالية يكون توزيعها مشابهاً للتوزيع الطبيعي خاصة إذا كان حجم العينة كبيراً.
هناك نوعان من الطرق الإحصائية التي تستخدم في اختبار الفرضيات:
( أ ) الاختبارات المعلمية: وتستخدم في حالة البيانات الرقمية التي توزيعها يتبع التوزيع الطبيعي.
(ب) الاختبارات غير المعلمية: وتستخدم في حالة البيانات الرقمية التي توزيعها لا يتبع التوزيع الطبيعي طبيعي، وكذلك في حالتي البيانات الترتيبية والوصفية.
2- صياغة فرضيتا العدم والبديلة
مثلاً: عند اختبار أن متوسط المجتمع يساوى قيمة معينة مقابل الفرضية القائلة بأن لا يساوى ، فإن فرضية العدم والفرضية البديلة تكون على النحو التالي:
3- اختيار مستوى المعنوية
4- اختيار دالة الاختبار الإحصائية المناسبة
5- جمع البيانات من العينة وحساب قيمة دالة الاختبار الإحصائية
6- اتخاذ القرارات
نرفض ونقبلإذا كانت قيمة الاحتمال (Sig. or P-value) أقل من أو تساوي مستوى المعنوية ()، أما إذا كانت قيمة الاحتمال أكبر من فلا يمكن رفض .
وبرنامج SPSS يعطي Sig. 2-tailed فبالتالي نرفض فرضية العدم عندما تكون .
أولاً: اختبار T في حالة اختبار فرضيات متعلقة بمتوسط واحد
إذا كان المطلوب اختبار فرضية العدم على مستوى دلالة مقابل
مثال (1)
البيانات التالية تمثل درجات عشرين طالباً في مساق ما:
65, 72, 68, 82, 45, 92, 87, 85, 90, 60, 48, 60, 68, 72, 79, 68, 73, 69, 78, 84
المطلوب: اختبار الفرضية المبدئية القائلة بأن متوسط درجات الطلاب = 65 درجة.
SPSS STEP BY STEP
Analyze Compare Means One-Sample T Test
ثانياً: اختبارات الفروق بين متوسطين مجتمعين مستقلين
في هذه الحالة نأخذ عينة عشوائية من توزيع طبيعي ، وعينة عشوائية أيضاً من توزيع طبيعي ومستقل عن التوزيع الأول، وتكون ولكنهما مجهولتان.
إذا كان المطلوب اختبار فرضية العدم على مستوى دلالة مقابل
مثال (2)
مستخدماً الملف employee. المطلوب اختبار ما إذا كان هناك فرق معنوي بين متوسط الراتب الحالي السنوي للموظفين (salary) يعزى إلى متغير الجنس (gender) مستخدماً مستوى معنوية.
SPSS STEP BY STEP
Analyze Compare Means Independent- Samples T Test
ثالثاً: اختبارات الفروق بين متوسطي مجتمعين من عينات مرتبطة
في هذه الحالة تكون البيانات مزدوجة، أي أن العينتين مرتبطتان حيث أن البيانات تكون على شكل أزواج وبالتالي فإن حجم العينتين لابد أن يكون متساوياً.
مثال (3)
البيانات التالية تمثل نتائج تجربة أجريت على عشرين شخصاً لاختبار مدى فعالية نظام خاص من الغذاء لتخفيف الوزن، حيث تم قياس أوزانهم قبل البدء في تطبيق هذا النظام، وبعد اتباع هذا النظام الخاص لمدة ثلاثة شهور.
تحليل التباينAnalysis of Variance (ANOVA)
في هذه الحالة يكون الاهتمام مركزاً على دراسة تأثير عامل واحد له عدد من المستويات المختلفة وعند كل مستوى تكرر التجربة عدد من المرات، فمثلاً إذا أردنا اختبار ما إذا كانت هناك فروق بين ثلاثة أساليب لتدريس مساق الإحصاء مثلاً، ويكون المطلوب بحث ما إذا كانت هذه الأساليب لها تأثيرات متساوية في درجة تحصيل الطالب مع ملاحظة أن وجود اختلاف بين درجات الطلاب قد يرجع إلى عدة عوامل أخرى منها الفروق الفردية وعدد ساعات الدراسة وعدد أفراد الأسرة مثلاً أو غيرها من العوامل الأخرى.
أولاً: تحليل التباين الأحادي One-Way ANOVA
في أسلوب تحليل التباين يعطي نتائج جيدة إذا تحققت الشروط التالية:
المتغيرات (قيمة مفردات الظاهرة) مستقلة ولها توزيع طبيعي بنفس قيمة التباين.
مجموعة البيانات في المستويات المختلفة تشكل عينات عشوائية مستقلة ولها تباين مشترك
فإذا لم تتحقق هذه الشروط يمكن استخدام الاختبارات غير المعلمية
تحت الفروض السابقة، فإن الاختلاف الكلي المشاهد في مجموعة البيانات ينقسم إلى مركبتين الأولى نتيجة العامل والثانية للخطأ التجريبي.
ويكون المطلوب في تحليل التباين الأحادي اختبار الفرضية المبدئية أنه لا يوجد فروق بين متوسطات المجتمعات على مستوى دلالة .
بفرض أن العامل المراد دراسته له r من المستويات المستقلة فيكون المطلوب اختبار الفرضية المبدئية (فرضية العدم): أي أنه لا يوجد فروق بين متوسطات المجتمعات.
مقابل الفرضية البديلة:
يوجد متوسطين على الأقل من أوساط المجتمعات غير متساويين أي أنه يوجد فروق بين متوسطات المجتمعات.
عند رفض فرضية العدم والتي تنص على تساوي المتوسطات وقبول الفرضية البديلة أنه يوجد اثنين أو أكثر من المتوسطات غير المتساوية، ونريد اختبار أي من هذه المتوسطات متساوٍ أو غير متساوٍ، وللإجابة على هذا التساؤل سنعرض عدة اختبارات.
لتنفيذ ذلك عملياً اضغط Post - Hoc في نافذة One-Way ANOVA.
مثال (4)
يمثل الجدول التالي درجات مجموعة من الطلبة تم تدريسهم مساق مبادئ الرياضيات العامة بثلاثة أساليب مختلفة:
المطلوب:
إدخال البيانات السابقة في متغير اسمه (marks).
إنشاء متغير جديد اسمه (factor) له ثلاثة قيم، (1) تمثل الأسلوب الأول، (2) تمثل الأسلوب الثاني و (3) تمثل الأسلوب الثالث.
هل هناك فرقاً بين أساليب التدريس الثلاثة مستخدماً مستوى دلالة ؟
الحل العملي:
SPSS STEP BY STEP
Analyze Compare Means One-Way ANOVA
ثانياً: تحليل التباين الثنائي Two-Way ANOVA
مثال (1):
يمثل الجدول التالي عدد الوحدات المنتجة في الأسبوع وذلك لعشرة عمال باستخدام ثلاثة أنواع مختلفة من الماكينات
المطلوب اختبار:
أ ) ما إذا كان العمال متساويين في الإنتاج.
ب) ما إذا كانت الماكينات متساوية في الإنتاج مستخدماً مستوى دلالة
ثالثاً: تحليل التباين الثلاثي Three-Way ANOVA
يستخدم تحليل التباين الثلاثي في حالة تجارب يؤثر عليها ثلاثة عوامل A,B,C مثلاً.
هناك سبعة اختبارات في حالة تحليل التباين الثلاثي مع وجود تفاعل بين العوامل الثلاثة وهي:
اختبار الفرضية : لا يوجد فروق بين متوسطات مستويات العامل الأول A.
اختبار الفرضية : لا يوجد فروق بين متوسطات مستويات العامل الثاني B.
اختبار الفرضية : لا يوجد فروق بين متوسطات مستويات العامل الثالث C.
اختبار الفرضية : لا يوجد تفاعل بين العاملين الأول والثاني A,B.
اختبار الفرضية : لا يوجد تفاعل بين العاملين الأول والثالث A,C .
اختبار الفرضية : لا يوجد تفاعل بين العاملين الثاني والثالث B,C.
اختبار الفرضية : لا يوجد تفاعل بين العوامل الثلاثة A,B,C.
مثال (5):
عند إنتاج مادة معينة. كان هناك ثلاثة عوامل مهمة وهى: A: تأثير المهندس (هناك ثلاثة مهندسين) B: المادة المساعدة على إنتاج المادة المطلوبة (هناك ثلاثة أنواع من المواد المساعدة) C: زمن التعبئة بعد الإنتاج (هناك فترتان 15 دقيقة و 20 دقيقة). يمثل الجدول التالي نتائج تجربة أجريت لهذا الغرض.
المطلوب:
كوِّن جدول تحليل التباين الثلاثي ثم فسَُر النتائج الكاملة التي يمكن الحصول عليها منه
Univariate Analysis of Variance
أولاً: تحليل التباين الأحادي One-Way ANOVA
في أسلوب تحليل التباين يعطي نتائج جيدة إذا تحققت الشروط التالية:
المتغيرات (قيمة مفردات الظاهرة) مستقلة ولها توزيع طبيعي بنفس قيمة التباين.
مجموعة البيانات في المستويات المختلفة تشكل عينات عشوائية مستقلة ولها تباين مشترك
فإذا لم تتحقق هذه الشروط يمكن استخدام الاختبارات غير المعلمية
تحت الفروض السابقة، فإن الاختلاف الكلي المشاهد في مجموعة البيانات ينقسم إلى مركبتين الأولى نتيجة العامل والثانية للخطأ التجريبي.
ويكون المطلوب في تحليل التباين الأحادي اختبار الفرضية المبدئية أنه لا يوجد فروق بين متوسطات المجتمعات على مستوى دلالة .
بفرض أن العامل المراد دراسته له r من المستويات المستقلة فيكون المطلوب اختبار الفرضية المبدئية (فرضية العدم): أي أنه لا يوجد فروق بين متوسطات المجتمعات.
مقابل الفرضية البديلة:
يوجد متوسطين على الأقل من أوساط المجتمعات غير متساويين أي أنه يوجد فروق بين متوسطات المجتمعات.
عند رفض فرضية العدم والتي تنص على تساوي المتوسطات وقبول الفرضية البديلة أنه يوجد اثنين أو أكثر من المتوسطات غير المتساوية، ونريد اختبار أي من هذه المتوسطات متساوٍ أو غير متساوٍ، وللإجابة على هذا التساؤل سنعرض عدة اختبارات.
لتنفيذ ذلك عملياً اضغط Post - Hoc في نافذة One-Way ANOVA.
مثال (4)
يمثل الجدول التالي درجات مجموعة من الطلبة تم تدريسهم مساق مبادئ الرياضيات العامة بثلاثة أساليب مختلفة:
70 | 64 | 48 |
83 | 45 | 94 |
87 | 56 | 83 |
78 | 50 | 84 |
71 | 80 | |
87 | ||
90 |
المطلوب:
إدخال البيانات السابقة في متغير اسمه (marks).
إنشاء متغير جديد اسمه (factor) له ثلاثة قيم، (1) تمثل الأسلوب الأول، (2) تمثل الأسلوب الثاني و (3) تمثل الأسلوب الثالث.
هل هناك فرقاً بين أساليب التدريس الثلاثة مستخدماً مستوى دلالة ؟
الحل العملي:
SPSS STEP BY STEP
Analyze Compare Means One-Way ANOVA
ثانياً: تحليل التباين الثنائي Two-Way ANOVA
مثال (1):
يمثل الجدول التالي عدد الوحدات المنتجة في الأسبوع وذلك لعشرة عمال باستخدام ثلاثة أنواع مختلفة من الماكينات
10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | العامل نوع الماكينة |
74 | 83 | 94 | 68 | 76 | 60 | 90 | 70 | 80 | 90 | 1 |
80 | 68 | 82 | 79 | 65 | 50 | 70 | 60 | 92 | 82 | 2 |
68 | 93 | 71 | 86 | 92 | 90 | 80 | 82 | 65 | 76 | 3 |
المطلوب اختبار:
أ ) ما إذا كان العمال متساويين في الإنتاج.
ب) ما إذا كانت الماكينات متساوية في الإنتاج مستخدماً مستوى دلالة
ثالثاً: تحليل التباين الثلاثي Three-Way ANOVA
يستخدم تحليل التباين الثلاثي في حالة تجارب يؤثر عليها ثلاثة عوامل A,B,C مثلاً.
هناك سبعة اختبارات في حالة تحليل التباين الثلاثي مع وجود تفاعل بين العوامل الثلاثة وهي:
اختبار الفرضية : لا يوجد فروق بين متوسطات مستويات العامل الأول A.
اختبار الفرضية : لا يوجد فروق بين متوسطات مستويات العامل الثاني B.
اختبار الفرضية : لا يوجد فروق بين متوسطات مستويات العامل الثالث C.
اختبار الفرضية : لا يوجد تفاعل بين العاملين الأول والثاني A,B.
اختبار الفرضية : لا يوجد تفاعل بين العاملين الأول والثالث A,C .
اختبار الفرضية : لا يوجد تفاعل بين العاملين الثاني والثالث B,C.
اختبار الفرضية : لا يوجد تفاعل بين العوامل الثلاثة A,B,C.
مثال (5):
عند إنتاج مادة معينة. كان هناك ثلاثة عوامل مهمة وهى: A: تأثير المهندس (هناك ثلاثة مهندسين) B: المادة المساعدة على إنتاج المادة المطلوبة (هناك ثلاثة أنواع من المواد المساعدة) C: زمن التعبئة بعد الإنتاج (هناك فترتان 15 دقيقة و 20 دقيقة). يمثل الجدول التالي نتائج تجربة أجريت لهذا الغرض.
المطلوب:
كوِّن جدول تحليل التباين الثلاثي ثم فسَُر النتائج الكاملة التي يمكن الحصول عليها منه
Univariate Analysis of Variance
الاختبارات غير المعلمية Nonparametric Tests
في بعض الحالات قد لا تتوافر في المجتمع موضع الدراسة أن يكون توزيع هذا المجتمع له توزيع طبيعي أو يقترب منه، لذلك فإن استخدام الاختبارات المعلمية في مثل هذه الحالات قد يؤدي إلى نتائج غير دقيقة، كذلك يفترض أن تكون بيانات الظاهرة موضع الدراسة دقيقة، ولكن في بعض الأحيان يتعذر أخذ قياسات عددية دقيقة على بعض الظواهر، لذلك فإننا نستخدم طرق غير معلمية لا تعتمد على شروط معينة تتعلق بتوزيع المجتمع ولا تحتاج إلى قياسات دقيقة.
مزايا استخدام الاختبارات غيرالمعلمية:
1ـ سهولة العمليات الحسابية المستخدمة.
2ـ لا تحتاج إلى شروط كثيرة لذلك فإن إمكانية إساءة استعمالها قليلة جداً.
3ـ تستخدم عندما لا تتحقق الشروط اللازمة لتطبيق الاختبارات المعلمية مثل أن يكون توزيع المجتمع طبيعياً.
4ـ تستخدم في حالة صعوبة الحصول على بيانات دقيقة.
5ـ لا يتطلب استخدامها معرفة دقيقة في مجال الرياضيات أو الإحصاء.
6ـ لا تشترط استخدامها أن يكون حجم العينات كبيراً، لذلك فإن عملية جمع البيانات في هذه الحالة توفر الوقت والمجهود والتكلفة.
عيوب استخدام الاختبارات غيرالمعلمية:
1ـ تستخدم أحياناً في الحالات التي يجب استخدام الاختبارات المعلمية وذلك لسهولة استخدامها.
2ـ صعوبة الحصول على توزيع دوال الاختبار المستخدمة في هذه الاختبارات.
يمكن استخدام الاختبارات غيرالمعلمية في الحالات التالية:
1ـ للحصول على قرار سريع.
2ـ إذا كانت البيانات المتوفرة عن ظاهرة ما لا تتفق مع الاختبارات المعلمية.
3ـ إذا كانت الشروط المطلوب توافرها في الاختبار المعلمي غير متحققة.
سنعرض فيما يلي استخدام برنامج SPSSفي الاختبارات غيرالمعلمية التالية:
1ـ استخدام اختبار كولمجروف – سمرنوف "One-Sample Kolmogorov-Smirnov Test" لمعرفة ما إذا كانت البيانات تتبع التوزيع الطبيعي.
ا2ـ ختبار الإشارة "Sign Test"لاختبار فرضيات حول متوسط مجتمع واحد.
3ـ اختبار ويلكوكسن "Wilcoxon Test" لاختبار فرضيات حول مقارنة متوسطي مجتمعين في حالة العينات المرتبطة.
ا4ـ ختبار مان – وتني "Mann Whitney Test" لاختبار الفرضيات حول الفرق بين متوسطي مجتمعين في حالة العينات المستقلة.
5ـ اختبار كروسكال – والاس "Kruskal-Wallis Test"لاختبار فرضيات لمقارنة متوسطات عدة مجتمعات مستقلة (تحليل التباين في حالة العينات المستقلة).
6ـ اختبار فريدمان "Friedman Test"الذي يعالج موضوع تحليل التباين في حالة المشاهدات المتكررة (Repeated Measures)أو العينات المرتبطة .
مزايا استخدام الاختبارات غيرالمعلمية:
1ـ سهولة العمليات الحسابية المستخدمة.
2ـ لا تحتاج إلى شروط كثيرة لذلك فإن إمكانية إساءة استعمالها قليلة جداً.
3ـ تستخدم عندما لا تتحقق الشروط اللازمة لتطبيق الاختبارات المعلمية مثل أن يكون توزيع المجتمع طبيعياً.
4ـ تستخدم في حالة صعوبة الحصول على بيانات دقيقة.
5ـ لا يتطلب استخدامها معرفة دقيقة في مجال الرياضيات أو الإحصاء.
6ـ لا تشترط استخدامها أن يكون حجم العينات كبيراً، لذلك فإن عملية جمع البيانات في هذه الحالة توفر الوقت والمجهود والتكلفة.
عيوب استخدام الاختبارات غيرالمعلمية:
1ـ تستخدم أحياناً في الحالات التي يجب استخدام الاختبارات المعلمية وذلك لسهولة استخدامها.
2ـ صعوبة الحصول على توزيع دوال الاختبار المستخدمة في هذه الاختبارات.
يمكن استخدام الاختبارات غيرالمعلمية في الحالات التالية:
1ـ للحصول على قرار سريع.
2ـ إذا كانت البيانات المتوفرة عن ظاهرة ما لا تتفق مع الاختبارات المعلمية.
3ـ إذا كانت الشروط المطلوب توافرها في الاختبار المعلمي غير متحققة.
سنعرض فيما يلي استخدام برنامج SPSSفي الاختبارات غيرالمعلمية التالية:
1ـ استخدام اختبار كولمجروف – سمرنوف "One-Sample Kolmogorov-Smirnov Test" لمعرفة ما إذا كانت البيانات تتبع التوزيع الطبيعي.
ا2ـ ختبار الإشارة "Sign Test"لاختبار فرضيات حول متوسط مجتمع واحد.
3ـ اختبار ويلكوكسن "Wilcoxon Test" لاختبار فرضيات حول مقارنة متوسطي مجتمعين في حالة العينات المرتبطة.
ا4ـ ختبار مان – وتني "Mann Whitney Test" لاختبار الفرضيات حول الفرق بين متوسطي مجتمعين في حالة العينات المستقلة.
5ـ اختبار كروسكال – والاس "Kruskal-Wallis Test"لاختبار فرضيات لمقارنة متوسطات عدة مجتمعات مستقلة (تحليل التباين في حالة العينات المستقلة).
6ـ اختبار فريدمان "Friedman Test"الذي يعالج موضوع تحليل التباين في حالة المشاهدات المتكررة (Repeated Measures)أو العينات المرتبطة .
الارتباط الخطي البسيط Simple Linear Regression
في معظم التطبيقات العملية نجد أن هناك علاقة بين متغيرين (أو أكثر)، فمثلاً نجد أن هناك علاقة وارتباط بين درجة الطالب وعدد ساعات الدراسة. يوجد نوعان من المتغيرات هما:
المتغير التابع Dependent (Response) Variable: هو المتغير الذي يقيس نتيجة دراسة ما، وعادة يرمز له بالرمز Y.
المتغير المستقل Independent (Explanatory) Variable:
هو المتغير الذي يُفسِّر أو يسبب التغيرات في المتغير التابع، أي هو الذي يؤثر في تقدير قيمة المتغير التابع، وعادة يرمز له بالرمز X. فمثلاً عدد أيام الغياب X و درجة الطالب في الإحصاء Y، العُمر Xوالإصابة بضغط الدم Y.
في بعض التطبيقات العملية يكون لدينا أكثر من متغيرين تحت الدراسة، فمثلاً قد توجد علاقة خطية بين ضغط الدم وكل من العُمر والوزن، ويسمى الارتباط في هذه الحالة الارتباط الخطي المتعدد.
عند دراسة العلاقة بين متغيرين X, Y فإن شكل الانتشار Scatter plot يمكن أن يوضح طبيعة هذه العلاقة، وتكون العلاقة بين X, Y قوية جداً إذا وقعت معظم نقاط شكل الانتشار على منحنى أو خط مستقيم، وتكون ضعيفة كلما تناثرت نقاط شكل الانتشار حول منحنى أو خط مستقيم يمر بتلك النقاط.
معامل الارتباط Correlation Coefficient:
هو مقياس لدرجة العلاقة بين المتغيرين Y, X ويرمز له بالرمز r، ويحقق معامل الارتباط الخطي المتباينة:
أي أن قيمة معامل الارتباط محصورة بين ، وتدل قيمته على درجة العلاقة بين المتغيرين أو المتغيرات موضع الدراسة من حيث أنها قوية، متوسطة، أو ضعيفة، وأما الإشارة فإنها تصف نوعية العلاقة هل هي عكسية أم طردية، فالإشارة السالبة تدل على وجود علاقة عكسية أما الموجبة فتدل على وجود علاقة طردية بين المتغيرين موضع الدراسة.
إذا كانت قيمة معامل الارتباط مساوية للواحد الصحيح فهذا يدل على أن الارتباط بين المتغيرين ارتباطاً طردياً تاماً، أما إذا كانت قيمته مساوية لـ فهذا يدل على أن الارتباط بين المتغيرين ارتباطاً عكسياً تاماً.
إذا كانت قيمة معامل الارتباط مساوية للصفر(r = 0 ( فهذا يدل على عدم وجود ارتباط خطي بين المتغيرين موضع الدراسة، بمعنى أنه إذا عرفنا اتجاه تغير أحد المتغيرين استحال علينا تحديد أو معرفة اتجاه المتغير الآخر.
أما إذا ابتعدت بعض نقاط شكل الانتشار عن الخط المستقيم فإن الارتباط يكون غير تاماً، وتزداد قوة الارتباط كلما اقتربت قيمة r من القيمة أو القيمة . فمثلاً الطول والوزن لمجموعة من الأشخاص قد يوجد بينها ارتباطاً طردياً ولكن ليس ارتباطاً تاماً. العلاقة بين X, Y تكون:
طردية ضعيفة عندما .
طردية متوسطة عندما .
طردية قوية عندما
عكسية ضعيفة عندما
عكسية متوسطة عندما عكسية قوية عندما
المتغير التابع Dependent (Response) Variable: هو المتغير الذي يقيس نتيجة دراسة ما، وعادة يرمز له بالرمز Y.
المتغير المستقل Independent (Explanatory) Variable:
هو المتغير الذي يُفسِّر أو يسبب التغيرات في المتغير التابع، أي هو الذي يؤثر في تقدير قيمة المتغير التابع، وعادة يرمز له بالرمز X. فمثلاً عدد أيام الغياب X و درجة الطالب في الإحصاء Y، العُمر Xوالإصابة بضغط الدم Y.
في بعض التطبيقات العملية يكون لدينا أكثر من متغيرين تحت الدراسة، فمثلاً قد توجد علاقة خطية بين ضغط الدم وكل من العُمر والوزن، ويسمى الارتباط في هذه الحالة الارتباط الخطي المتعدد.
عند دراسة العلاقة بين متغيرين X, Y فإن شكل الانتشار Scatter plot يمكن أن يوضح طبيعة هذه العلاقة، وتكون العلاقة بين X, Y قوية جداً إذا وقعت معظم نقاط شكل الانتشار على منحنى أو خط مستقيم، وتكون ضعيفة كلما تناثرت نقاط شكل الانتشار حول منحنى أو خط مستقيم يمر بتلك النقاط.
معامل الارتباط Correlation Coefficient:
هو مقياس لدرجة العلاقة بين المتغيرين Y, X ويرمز له بالرمز r، ويحقق معامل الارتباط الخطي المتباينة:
أي أن قيمة معامل الارتباط محصورة بين ، وتدل قيمته على درجة العلاقة بين المتغيرين أو المتغيرات موضع الدراسة من حيث أنها قوية، متوسطة، أو ضعيفة، وأما الإشارة فإنها تصف نوعية العلاقة هل هي عكسية أم طردية، فالإشارة السالبة تدل على وجود علاقة عكسية أما الموجبة فتدل على وجود علاقة طردية بين المتغيرين موضع الدراسة.
إذا كانت قيمة معامل الارتباط مساوية للواحد الصحيح فهذا يدل على أن الارتباط بين المتغيرين ارتباطاً طردياً تاماً، أما إذا كانت قيمته مساوية لـ فهذا يدل على أن الارتباط بين المتغيرين ارتباطاً عكسياً تاماً.
إذا كانت قيمة معامل الارتباط مساوية للصفر(r = 0 ( فهذا يدل على عدم وجود ارتباط خطي بين المتغيرين موضع الدراسة، بمعنى أنه إذا عرفنا اتجاه تغير أحد المتغيرين استحال علينا تحديد أو معرفة اتجاه المتغير الآخر.
أما إذا ابتعدت بعض نقاط شكل الانتشار عن الخط المستقيم فإن الارتباط يكون غير تاماً، وتزداد قوة الارتباط كلما اقتربت قيمة r من القيمة أو القيمة . فمثلاً الطول والوزن لمجموعة من الأشخاص قد يوجد بينها ارتباطاً طردياً ولكن ليس ارتباطاً تاماً. العلاقة بين X, Y تكون:
طردية ضعيفة عندما .
طردية متوسطة عندما .
طردية قوية عندما
عكسية ضعيفة عندما
عكسية متوسطة عندما عكسية قوية عندما
حساب قيمة معامل الارتباط:
يمكن حساب قيمة معامل الارتباط بعدة طرق مختلفة تبعاً لنوع البيانات.
الارتباط بين المتغيرات الرقمية: معامل بيرسون للارتباط.
الارتباط بين المتغيرات الترتيبية: معامل سبيرمان للرتب
الارتباط بين المتغيرات الوصفية: مربع كاي Chi-Square.
مثال (5)
افتح الملف Employee Data. المطلوب إيجاد قيمة معامل الارتباط الخطي بين كلاً من المتغيرات salary, salbegin, educ
SPSS STEP BY STEP
Analyze Correlate Bivariate
الارتباط بين المتغيرات الرقمية: معامل بيرسون للارتباط.
الارتباط بين المتغيرات الترتيبية: معامل سبيرمان للرتب
الارتباط بين المتغيرات الوصفية: مربع كاي Chi-Square.
مثال (5)
افتح الملف Employee Data. المطلوب إيجاد قيمة معامل الارتباط الخطي بين كلاً من المتغيرات salary, salbegin, educ
SPSS STEP BY STEP
Analyze Correlate Bivariate
الانحدار الخطي البسيط Simple Linear Regression
الانحدار هو دراسة للتوزيع المشترك لمتغيرين أحدهما متغير يقاس دون خطأ ويسمى متغير مستقل Independent variable ويرمز له بالرمز والآخر يأخذ قيماً تعتمد على قيمة المتغير المستقل ويسمى التابع Dependent variable ويرمز له بالرمز.
الهدف من دراسة الانحدار هو إيجاد دالة العلاقة بين المتغيرين المستقل والتابع والتي تساعد في تفسير التغير الذي قد يطرأ على المتغير التابع () تبعاً لتغير في قيم المتغير المستقل ().
مثال (7)
لدراسة العلاقة بين الدخل والاستهلاك بالدنانير في مدينة غزة، أخذت عينة مكونة من عشرة أسر فأعطت النتائج التالية:
المطلوب: إيجاد نموذج انحدار الاستهلاك على الدخل.
SPSS STEP BY STEP
Analyze Regression Linear
الهدف من دراسة الانحدار هو إيجاد دالة العلاقة بين المتغيرين المستقل والتابع والتي تساعد في تفسير التغير الذي قد يطرأ على المتغير التابع () تبعاً لتغير في قيم المتغير المستقل ().
مثال (7)
لدراسة العلاقة بين الدخل والاستهلاك بالدنانير في مدينة غزة، أخذت عينة مكونة من عشرة أسر فأعطت النتائج التالية:
الدخل | 300 | 350 | 500 | 600 | 900 | 1000 | 900 | 1200 | 1050 | 250 |
الاستهلاك | 280 | 340 | 500 | 550 | 800 | 750 | 850 | 1050 | 1000 | 250 |
المطلوب: إيجاد نموذج انحدار الاستهلاك على الدخل.
SPSS STEP BY STEP
Analyze Regression Linear






